programming musings

Introduction: lists galore

I learned programming backwards, plunging right on into C and, shortly after, C++ and Java from the very beginning. I was knee deep in complex data structures, pointers and abstruse template syntax in no time. And the more complex it all felt, the more i thought i was learning. Of course, i was clueless.

Reading SICP and learning about functional programming changed it all. There were many occasions for revelation and awe, but one of my most vivid recollections of that time is my gradual discovery of the power of simplicity. At about half way into SICP i realised in wonder that that beautiful and powerful world was apparently being constructed out of extremely simple pieces. Basically, everything was a list. Of course there were other important ingredients, like procedures as first-class objects, but the humble list was about the only data structure to be seen. After mulling on it for a little bit, i saw where lists draw their power from: recursion. As you know, lists are data types recursively defined: a list is either the empty list or an element (its head) followed by another list (its tail):

list = []

list = a : list

where i’m borrowing Haskell’s notation for the empty list ([]) and the list constructor (:), also known by lispers as () and cons. So that was the trick, i thought: lists have recursion built-in, so to speak, and once you’ve read a little bit about functional programming you don’t need to be sold on the power and beauty of recursive programs.

It is often the case that powerful and beautiful yet simple constructs have a solid mathematical foundation, and only when you grasp it do you really realize how powerful, beautiful and amazingly simple that innocent-looking construct is. Lists, and recursive operations on them, are an excellent case in point. But the path connecting them to their mathematical underpinnings is a long and winding one, which lays in the realm of Category Theory.

I first became acquainted of the relationship between categories and recursive programming reading Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire, by Erik Meijer, Maarten Fokkinga and Ross Paterson. Albeit very enjoyable, this paper presupposes a high degree of mathematical sophistication on the reader’s side. I will try in this article to give you a simplified overview of the concepts involved, including Category Theory, its application to programming languages and what funny names like catamorphism, anamorphism or lambda-lifting have to do with your everyday list manipulations. Of course, i’ll be only scratching the surface: interspersed links and the Further reading section provide pointers to more in-depth explorations of this wonderland.

Categorical interlude

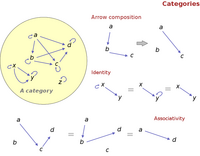Categories are (relatively) simple constructs. A category consists of a set O of objects, and a set A of arrows between elements of O. Arrows are composable: if there’s an arrow from a to b, and another one from b to c, there must be an arrow from a to c (where a, b and c are elements of O). Besides, they are associative: if you have arrows from a to b, b to c, and c to d, you can go from a to d via two different paths, namely, first from a to c and then from c to d, or first from a to b and then from b to d. Finally, for each element a in O there’s an identity arrow which goes from a to itself (called an identity), such that following this arrow changes nothing. These properties are better visualized with a diagram (or a bit of mathematical notation), as shown in the image on the right.

A category captures a mathematical world of objects and their relationships. The canonical example of a category is Set, which contains, as objects, (finite) sets and, as arrows, (total) functions between them. But categories go far beyond modeling sets. For instance, one can define a category whose objects are natural numbers, and the ‘arrows’ are provided by the relation “less or equal” (that is, we say that there is an arrow joining two numbers a and b if a is less or equal than b). What we are trying to do with such a definition is to somehow capture the essence of ordered sets: not only integers are ordered but also dates, lemmings on a row, a rock’s trajectory or the types of the Smalltalk class hierarchy. In order to abstract what all those categories have in common we need a way to go from one category to another preserving the shared structure in the process. We need what the mathematicians call an isomorphism, which is the technically precise manner of stating that two systems are, in a deep sense, analogous; this searching for commonality amounts to looking for concepts or abstractions, which is what mathematics and (good) programming is all about (and, arguably, intelligence itself, if you are to believe, for instance, Douglas Hofstadter’s ideas).

To boot, our definition of a category already contains the concept of isomorphic objects. Think of an arrow from a to b as an operation that transforms a in b. An arrow from b to a will make the inverse transformation. If composing both transformations gives you the identity, you are back to the very same object a, and we say that a and b are isomorphic: you can transform one into the other and back at will. In a deep sense, this concept captures a generic way of expressing equality that pervades all maths: if you’re not afraid of a little bit of maths, Barry Mazur’s essay When is a thing equal to some other thing? is an excellent introduction to Category Theory with an emphasis in the concept of equality. Among many other things, you will learn how the familiar natural numbers can be understood as a category, or how an object is completely defined by the set of its transformations (and, therefore, how to actually get rid of objects and talk only of transformations; i know this is stretching and mixing metaphors (if not plain silly), but this stress in arrows, as opposed to objects, reminded me of Alan Kay’s insistence on focusing on messages rather than objects). Another introductory article with emphasis on categories as a means to capture sameness is R. Brown and T. Porter’s Category Theory: an abstract setting for analogy and comparison.

Not only objects inside a category can be transformed into each other. We reveal the common structure of two disjoint categories by means of a functor mapping across two categories. A functor consists of two functions: one that maps each object of the first category to an object in the second, and another one putting in correspondence arrows in one category with arrows in the second. Besides, these functions must preserve arrow composition. Let me spell this mathematically. Consider to categories, C and C’ with object sets O and O’ and arrow sets A and A’. A functor F mapping C to C’ will consist then of two functions (Fo, Fa); the first one taking elements of O to elements of O’:

Fo: O -> O’

Fo(a) in O’ for every a in O

and the second one taking arrows from A to arrows in A’:

Fa: A -> A’

Fa(f) in A’ for every f in A

and such that, if f is an arrow from a to b in C, Fa(f) is an arrow from Fo(a) to Fo(b) in C’. Moreover, we want that following arrows in C is ‘analogous’ to following them in C’, i.e., we demand that

Fa(fg) = Fa(f)Fa(g)

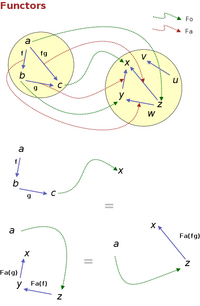In the left hand side above, we are composing two arrows in C and then going to C’, while in the right hand side we first take each arrow to C’ and, afterwards, compose them in there. If C and C’ have the same structure, these two operations must be equivalent. Finally, F must preserve identities: if i is the identity arrow for an element a in O, Fa(i)must be the identity arrow for Fo(a) in O’. The diagram on the left shows a partial graph (i’m not drawing the identity arrows and their mappings) of a simple functor between two categories, and ways of going from an object a in the first category to an object x in the second one which are equivalent thanks to the functor’s properties.

As you can see in this simple example, the functor gives us the ability of seeing the first category as a part of the second one. You get a category isomorphism in the same way as between objects, i.e., by demanding the existence of a second functor from C’ to C (you can convince yourself that such a functor does not exist in our example, and, therefore, that the two categories in the diagram are not isomorphic).

You have probably guessed by now one nifty property of functors: they let us going meta and define a category whose objects are categories and whose arrows are functors. Actually, Eilenberg and MacLane’s seminal paper General theory of natural transformations used functors and categories of categories to introduce for the first time categories (natural transformations are structure-preserving maps between functors: this Wikipedia article gives an excellent overview on them).

But enough maths for now: it is high time to show you how this rather abstract concepts find their place in our main interest, programming languages.

Categories and programming languages

About the only similarity between C and Haskell programming is that one spends a lot of time typing ASCII arrows. But of course, Haskell’s are much more interesting: you use them to declare the type of a function, as in

floor:: Real -> Int

The above stanza declares a function that takes an argument of type real and returns an integer. In general, a function taking a single argument is declared in Haskell following the pattern

fun:: a -> b

where a and b are types. Does this ring a bell? Sure it does: if we identify Haskell’s arrows with categorical ones, the language types could be the objects of a category. As we have seen, we need identities

id:: a -> a

id x = x

and arrow composition, which in Haskell is denoted by a dot

f:: b -> c

g:: a -> b

fg:: a -> b -> c

fg = f . g

Besides, associativity of arrow composition is ensured by Haskell’s referential transparency (no side-effects: if you preserve referential transparency by writing side-effect free functions, it won’t matter the order in which you call them): we’ve got our category. Of course, you don’t need Haskell, or a statically typed language for that matter: any strongly typed programming language can be modelled as a category, using as objects its types and as arrows its functions of arity one. It just happens that Haskell’s syntax is particularly convenient, but one can define function composition easily in any decent language; for instance in Scheme one would have

(define (compose f g) (lambda (x) (f (g x)))

Functions with more than one arguments can be taken into the picture by means of currying: instead of writing a function of, say, 2 arguments:

(define (add x y) (+ x y))

(add 3 4)

you define a function which takes one argument (x) and returns a function which, in turn, takes one argument (y) and returns the final result:

(define (add x) (lambda (y) (+ x y)))

((add 3) 4)

Again, Haskell offers a pretty convenient syntax. In Haskell, you can define add as:

add x y = x + y

which gets assigned, when applied to integers, the following type:

add:: Int -> (Int -> Int)

that is, add is not a function from pairs of integers to integers, but a function that takes an integer and returns a function of type Int -> Int. Finally, we can also deal with functions taking no arguments and constant values by introducing a special type, called unit or 1 (or void in C-ish), which has a unique value (spelled () in Haskell). Constants of our language (as, e.g., True or 43.23) are then represented by arrows from 1 to the constant’s type; for instance, True is an 1 -> Boolean arrow. The unit type is an example of what in category theory is known as a terminal object.

Now that we have successfully modelled our (functional) programming language as a category (call it C), we can use the tools of the theory to explore and reason about the language constructs and properties. For instance, functors will let me recover the original motivation of this post and explore lists and functions on them from the point of view of category theory. If our language provides the ability to create lists, its category will contain objects (types) of the ‘list of’ kind; e.g. [Int] for lists of integers, [Boolean] for lists of Booleans and so on. In fact, we can construct a new sub-category CL by considering list types as its objects and functions taking and returning lists as its arrows. For each type a we have a way of constructing a type, [a] in the sub-category, i.e., we have a map from objects in C to objects in CL. That’s already half a functor: to complete it we need a map from functions in C to functions in CL. In other words, we need a way to transform a function acting on values of a given type to a function acting on lists of values of the same type. Using the notation of the previous section:

Fo(a) = [a]

Fa(f: a -> b) = f': [a] -> [b]

Fa is better known as map in most programming languages. We call the process of going from f to f' lifting (not to be confused with a related, but not identical, process known as lambda lifting), and it’s usually pretty easy to write an operator that lifts a function to a new one in CL: for instance in Scheme we would write:

(define (lift f) (lambda (lst) (map f lst)))

and for lift to truly define a functor we need that it behaves well respect to function composition:

(lift (compose f g)) = (compose (lift f) (lift g))

We can convince ourselves that this property actually holds by means of a simple example. Consider the function next which takes an integer to its successor; its lifting (lift next) will map a list of integers to a list of their successors. We can also define prev and (lift prev) mapping (lists of) integers to (lists of) their predecessors. (compose next prev) is just the identity, and, therefore, (lift (compose next prev)) is the identity too (with lifted signature). But we obtain the same function if we compose (lift next) and (lift prev) in CL, right? As before, there’s nothing specific to Scheme in this discussion. Haskell even has a Functor type class capturing these ideas. The class defines a generic lift operation, called fmap that, actually, generalizes our list lifting to arbitrary type constructors:

fmap :: (a -> b) -> (f a -> f b)

where f a is the new type constructed from a. In our previous discussion, f a = [a], but if your language gives you a way of constructing, say, tuples, you can lift functions on given types to functions on tuples of those types, and repeat the process with any other type constructor at your disposal. The only condition to name it a functor, is that identities are mapped to identities and composition is preserved:

fmap id = id

fmap (p . q) = (fmap p) . (fmap q)

I won’t cover usage of type constructors (and their associated functors) other than lists, but just mention a couple of them: monads, another paradigmatic one beautifully (and categorically) discussed by Stefan Klinger in his Programmer’s Guide to the IO Monad – Don’t Panic (also discussed at LtU), and the creation of a dance and music library, for those of you looking for practical applications.

To be continued…

Returning to lists, what the lifting and categorical description above buys us is a way to formalize our intuitions about list operations, and to transfer procedures and patterns on simple types to lists. In SICP’s section on Sequences as conventional interfaces, you will find a hands-on, non-mathematical dissection of the basic building blocks into which any list operation can be decomposed: enumerations, accumulators, filters and maps. Our next step, following the bananas article i mentioned at the beginning, will be to use the language of category theory to provide a similar decomposition, but this time we will talk about catamorphisms, anamorphisms and similarly funny named mathematical beasts. What the new approach will buy us is the ability to generalize our findings beyond the list domain and onto the so-called algebraic types. But this will be the theme of a forthcoming post. Stay tunned.

Further reading

The best introductory text on Category Theory i’ve read is Conceptual Mathematics : A First Introduction to Categories by F. William Lawvere (one of the fathers of Category Theory) and Stephen Hoel Schanuel. It assumes no sophisticated mathematical background, yet it covers lots of ground. If you feel at home with maths, the best option is to learn from the horse’s mouth and get a copy of Categories for the Working Mathematician, by Mac Lane.

The books above do not deal with applications to Computer Science, though. For that, the canonical reference is Benjamin Pierce’s Basic Category Theory for Computer Scientists, but i find it too short and boring: a far better choice is, in my opinion, Barr and Well’s Category Theory and Computer Science. A reduced version of Barr and Well’s book is available online in the site for their course Introduction to Category Theory. They are also the authors of the freely available Toposes, Triples and Theories, which will teach you everything about monads, and then more. Marteen Fokkinga is the author of this 80-pages Gentle Introduction to Category Theory, with a stress on the calculational and algorithmical aspects of the theory. Unless you have a good mathematical background, you should probably take gentle with a bit of salt.

Let me close by mentioning a couple of fun applications of Category Theory, for those of you that know a bit about it. Haskell programmers will like this implementation of fold and unfold (as a literate program) using F-(co)algebras and applied to automata creation, while those of you with a soft spot for Physics may be interested in John Baez’s musings on Quantum Mechanics and Categories.

Tags: category theory, haskell, maths, metaprogramming, scheme